Jag inleder här en serie av inlägg på bloggen som kommer att förklara detaljerna kring de metoder som jag i huvudsak använder för mina riskanalyser. I ett tidigare inlägg har jag skrivit om vikten att jobba med sannolikhetsfördelningar i stället för enstaka värden. Allt arbete med statistik kräver att man har koll på diverse begrepp och förstår principerna bakom fördelningar. Se detta inlägg som en introduktion i ämnet.

Väntevärdet  E uttrycks även som medelvärdet och är det värde som utgör tyngdpunkten i en statistisk fördelning längs x-axeln. Väntevärdet är ett lägesmått.

Standardavvikelsen S är ett mått på en fördelnings spridning. Osäkerheten i en variabels värde uttrycks med dess standardavvikelse. Två variabler kan ha samma väntevärde men olikartade fördelningar, se figuren nedan.

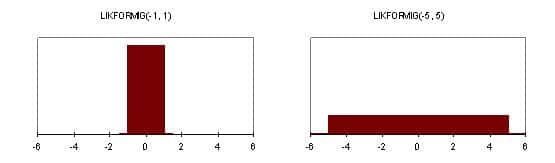
Om man jämför två likformiga fördelningar där den ena går från –1 och 1 och den andra från –5 och 5 inses att båda har väntevärdet 0, men det är uppenbart att den senare har en mer utspridd fördelning en den förra.

Variationskoefficenten VK, utgörs av kvoten mellan standardavvikelsen och väntevärdet, dvs VK = S/E. Variationskoefficienten anges ofta i procent.

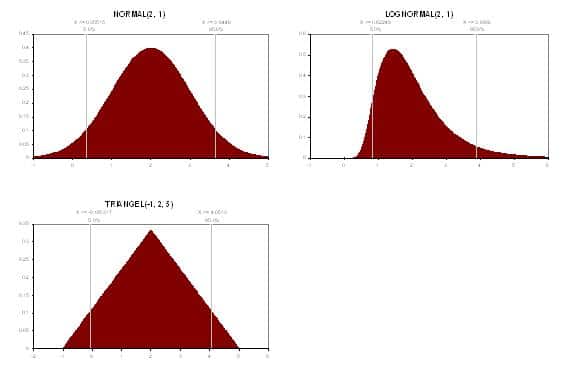
Statistiska fördelningar används för att beskriva osäkerheten i indata. Frantzich anger att det första som måste göras när dessa fördelningar skall skattas är att definiera fördelningens största och minsta värde. Därefter uppskattas väntevärde och varians. Slutligen skall en fördelning väljas som ger bästa tänkbara representation av variabeln. Vanliga fördelningar är normalfördelningen, lognormalfördelningen och triangelfördelningen. En grafisk illustration av dessa fördelningar visas i figuren nedan.