Jag har tidigare skrivit om vikten att hantera osäkerheter med statistiska fördelningar i stället för enstaka värden. I detta inlägg vill jag på ett enkelt sätt förklara hur Monte Carlo-metoden fungerar. Monte Carlo-simuleringar är en av de metoder vi använder för att kunna kombinera olika statistiska fördelningar och utför beräkningar med dessa. Föreställ dig följande: Riskområdet vid ett utsläpp av ammoniak ska beräknas. Längden på riskområdet består i huvudsak av utsläppets källstyrka (Q), vindhastigheten (u) och atmosfärens stabilitetsklass (sigma).

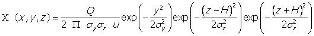
Ta fram tre urnor; en för källstyrkan, en för vindhastigheten och en för stabilitetsklassen. Lägg ner 100 papperslappar i varje med en siffra för dessa storheter. I källstyrkeurnan läggs det ner 20 lappar motsvarande källstyrkan för ett ”litet” hål, 50 lappar för ett ”medelstort” hål och 30 lappar för ett ”stort” hål. I vindhastighetsurnan ligger lappar från 1 m/s till 15 m/s, med de flesta lappar i intervallet 4-7 m/s. I den urnan som representerar stabilitetsklassen läggs det 10 lappar för instabil skiktning, 40 lappar för neutral skiktning och 50 lappar för stabil skiktning.

Vad man sedan gör är att man gör ett stort antal beräkningar av riskområdet med hjälp av de värden som kommer från succesiva dragningar från de tre urnorna. Efter varje dragning av de tre lapparna läggs dessa tillbaka i respektive urna, så att sannolikhetsfördelningarna för källstyrka, vindhastighet och stabilitetsklass förblir konstant. Exempel på dragningar från de 5 första dragningarna visas nedan:

För varje kombination av de tre värdena beräknas sedan riskområdet. Efter ett antal beräkningar kan man ta fram intressant statistisk information som histogram, CDF, CCDF mm. Detta kommer jag att skriva mer om i kommande inlägg.