
I tidigare inlägg har jag flaggat för att det är någon oegentlighet i MQH-metoden, närmare bestämt de beräkningar som redovisas i "Estimating Room Temperatures and the Likelihood of Flashover". Det hela började med att jag tyckte det var ruskigt knäppt att materialparametrar som ρck skulle spela så pass stor för den effekt som krävs för att orsaka övertändning i ett rum. Nedanstående räkneexempel talar för sig själv.
Om vi antar att 1 000 kW är en tillräckligt stor brand för att orsaka övertändning i ett rum med en viss storlek och omgivande ytor är av betong. Då skulle det endast krävas kring 130 kW för att orsaka övertändning om omgivande ytor är av mineralull. På samma sätt skulle det krävas 3 600 kW om väggarna var av aluminium. Beräkningarna är gjorda för karakteristiska värden på ρck för de olika materialen och ekvationen:
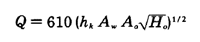
I artikeln redovisas följande figur där den effektutveckling som krävs för att orsaka övertändnig (ΔT=500 C) plottas för olika material och öppningsförhållanden.
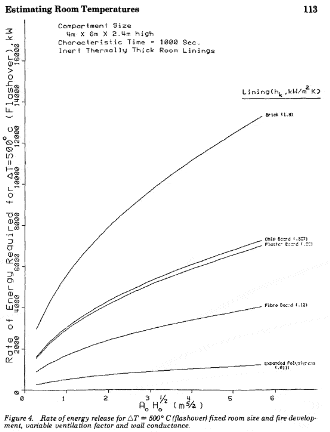
Beräkningarna gäller för ett rum på 4 m x 6 m x 2,4 m och en karakteristisk tid på 1 000 s, vilken används för att beräkna h(k) med hjälp av nedanstående ekvation:
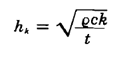
Beräknade värden på hk anges i figuren ovan:
”Brick wall” 1,3 kW/m2K
”Fibre board” 0,12 kW/m2K
Värdena på h(k) sägs vara beräknade med de materialdata (ρck) som anges i artikeln. Angivet ρck för “brick wall” är 1,7 (kW)^2 s/m^4/K^2 och för “fibre board” är det 0,015 (kW)^2 s/m^4/K^2. Om dessa värden skulle användas för att beräkna h(k) blir resultatet inte det samma som de värden på h(k) som anges i figuren ovan.
|
Material
|
ρck
|
h(k), beräknat med ρck
|
h(k), figuren
|
|
Brick wall
|
1,7 (kW)^2 s/m^4/K^2
|
0,041 kW/m2K
|
1,3 kW/m2K
|
|
Fibre board
|
0,015 (kW)^2 s/m^4/K^2
|
0,0039 kW/m2K
|
0,12 kW/m2K
|
Så här långt in i felsökningen kände jag för att dela med mig av mina “misstankar” och i ett snällt mail till Daniel Gojkovic, min f.d. kollega på ØSA bad jag honom gräva lite djupare. Det visade sig att lösningen på problemet inte var särskilt svår att finna. Om ni tittar på värdena i tabellen ovan för “brick wall” och “fibre board” så ser man att kvoten mellan h(k), figur och h(k) beräknat är c:a 31, dvs. samma som 1000^0,5.
Det finns åtminstone två tänkbara förklaringar till räknefelet. Antingen har författarna “glömt” att dividera med t (= 1 000 s) eller så har det blivit fel i övergången från (kW)^2 till W^2. Att använda 1000^2 hade varit korrekt, men man kan misstänka att författarna använt 1000^3. Oavsett vilket så har h(k) överskattats med en faktor 1000^0,5. vilket i slutändan blir en överskattning av Q med en faktor (1000^0,5)^0,5 = 5,6. Figuren ovan kan nu ritas om för att grafiskt visa betydelsen av “räknefelet”
![clip_image002[12] clip_image002[12]](https://wuz.se/wp-content/uploads/FelrknatiEstimatingRoomTemperaturesandth_8D3B/clip_image00212.gif)
Tyvärr tar det inte slut här. Det verkar vara ganska oklart hur A(w) i ekvationen ovan egentligen ska beräknas. Antingen omfattar A(w) alla ytor i rummet (inkl. öppningar) undantaget golvet, eller så är A(w) =
A(T) och omfattar alla ytor i rummet (inkl. öppningar och golvet).
Författarnas analys av data från de mer än 100 experiment som använts görs för två fall – med eller utan värmeledning via golvet. Uttrycket som sedan ligger till grund för ekvationen för Q utgörs av sammanviktning av regressionsanalyserna med- och utan hänsyn till värmeledning in i golvet. Skillnaden blir märkbar. Redan i ett mindre rum blir skillnaden påtaglig, se figuren nedan.
![clip_image002[17] clip_image002[17]](https://wuz.se/wp-content/uploads/FelrknatiEstimatingRoomTemperaturesandth_8D3B/clip_image00217.gif)
Skillnaden mellan den effekt (Q) som krävs för övertändning bestäms av kvadratroten av kvoten mellan den totala omslutningsytan A(T) och omslutningsytan undantaget golvet A(w), dvs (A(T)/A(w))^0,5. För lokalen i figuren ovan blir skillnaden en faktor 1,16. Om lokalen i stället skulle haft måtten 10 m x 20 m x 3 m blir skillnaden 1,24. Betydelsen av definitionen på omslutningsytan faller visserligen inom modellosäkerheten, men ett förtydligande hade trots detta varit intressant. En liten notis är att författarna inte tar med golvytan när det ritar figurerna i artikeln.
Slutsats
Nu är det bevisat att det finns räknefel i figurerna i artikeln "Estimating Room Temperatures and the Likelihood of Flashover". Den stora frågan är om detta räknefel också begåtts vid beräkning av h(k) för de experimentiella data som ligger bakom MQH-metoden. Om så är fallet så är det givet att MQH-metoden överskattar den effekt som krävs för övertändning med en faktor 5 till 6. Jag tror det är läge att försöka få en respons från författarna där bland Quintiere.




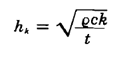
![clip_image002[12] clip_image002[12]](https://wuz.se/wp-content/uploads/FelrknatiEstimatingRoomTemperaturesandth_8D3B/clip_image00212.gif)
![clip_image002[17] clip_image002[17]](https://wuz.se/wp-content/uploads/FelrknatiEstimatingRoomTemperaturesandth_8D3B/clip_image00217.gif)


