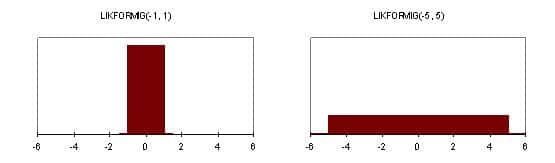
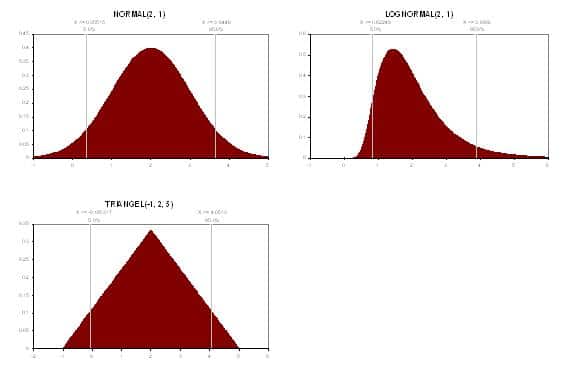
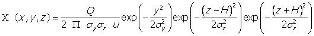Jag hade förmånen att få opponera på studenterna i Riskanalysmetoder och deras projektuppgift inom området ”säkerhet” i förra veckan. Uppgiften de fick var väldefinierad:
Avgör om en lagring av klorgas kan tillåtas på en industrifastighet i centrala Malmö
Med hjälp av beräkningar av individ-, medel- och samhällsrisk för tre bestämda scenarier skulle studenterna avgöra om lagring av klorgas kan tillåtas utifrån ett riskperspektiv. De tre scenarierna var:
- Tankens innehåll töms på 10 min (0,7×10-6 år-1)
- Tankutsläpp genom ett hål med diameter 10 mm. (1,1×10-5 år-1)
- Litet rörbrott (5 mm) (5×10-6 år-1m-1)
Resultatet skiljer kraftigt (!) mellan de olika grupperna. Jag har valt att redovisa spridningen med hjälp av några histogram. Den stora orsaken till spridningen är framförallt valet av stabilitetsklass och vindhastighet. De flesta grupper väljer att jobbar mycket konservativt med stabila atmosfärsförhållanden och låga vindhastigheter.
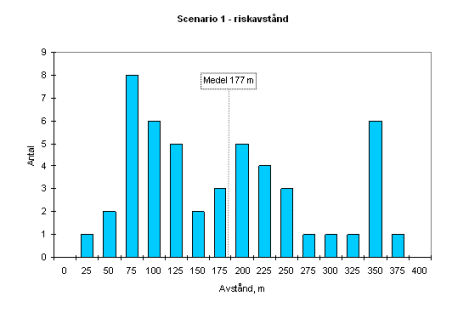
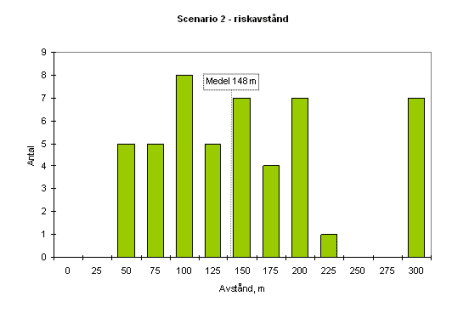
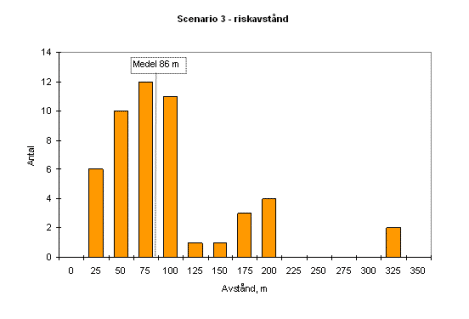 Â
Â
I kommande inlägg tänkte jag visa på spridningen i beräkningen av de olika riskmåtten.